Rarity Score 리뷰

Rarity Score : A New Metric to Evaluate the Uncommonness of Synthesized Images 리뷰

 

link : https://arxiv.org/pdf/2206.08549.pdf

 

ICLR 2023 top 25% 를 받는 metric 논문.

 

 

Intro

---

본 논문은 individual 이미지의 "rariry" 측정을 시도한 최초의 논문.  해당 novelty에서 우수한 평가를 받은듯 하다.

Exisiting metric들은 how well generated (Real의 distribution을 얼마나 잘 따라감) 을 타겟팅하는 반면 본 논문은 generated에서 만든 샘플이 얼마나 rare 한가를 측정함.

 

rarity가 높을수록 typicial 하지 않은 레어한 이미지가 나온다. + nonsense인 이미지는 없다.

 

Main contribution 요약

• Classify whether individual image is typical or rare.
• Compare SOTA GAN’s creativity without losing fidelity.
• Proposed metric can be applied on top of the various feature spaces (e.g. CLIP, DINO ..)

 

 

Preliminary

---

Preliminaries

• Precision/Recall (Tuomas Kynkäänniemi, Tero Karras, Samuli Laine, Jaakko Lehtinen, and Timo Aila. Improved precision and recall metric for assessing generative models. In NeurIPS, 2019.)
• Density/Coverage (Muhammad Ferjad Naeem, Seong Joon Oh, Youngjung Uh, Yunjey Choi, and Jaejun Yoo. Reliable fidelity and diversity metrics for generative models. In ICML, 2020.)
• Realism score
  (펼치면 prdc recap)

 

Precision : real의 manifold에 generated가 얼마나 속하는지 (generated의 fidelity 측정)

Recall : generated의 manifold에 real이 얼마나 속하는지 (real의 diversity 측정)

 

Density : Indicator를 G, R 에 모두 돌림. 즉 generated가  real의 hypersphere에 여러번 들어가는 경우도 중복으로 카운팅 허용, precision의 진화 버전.

 

Coverage : Real의 hypersphere에 한 번이라도 generated가 들어오면 카운팅. (recall 진화 버전)

(density와 달리 generated의 매니폴드 관점에서 측정함.. 만약 좋은 g라면 다양한 g 매니폴드에 generated samples들이 쏙쏙 박히므로 diversity가 좋을것.. 다시말해 coverage 굿일것)

(recall과 달리 real의 manifold만 구성하면 되므로 computational cost 감소)

 

Realism score is high when generated image looks real.

 

 

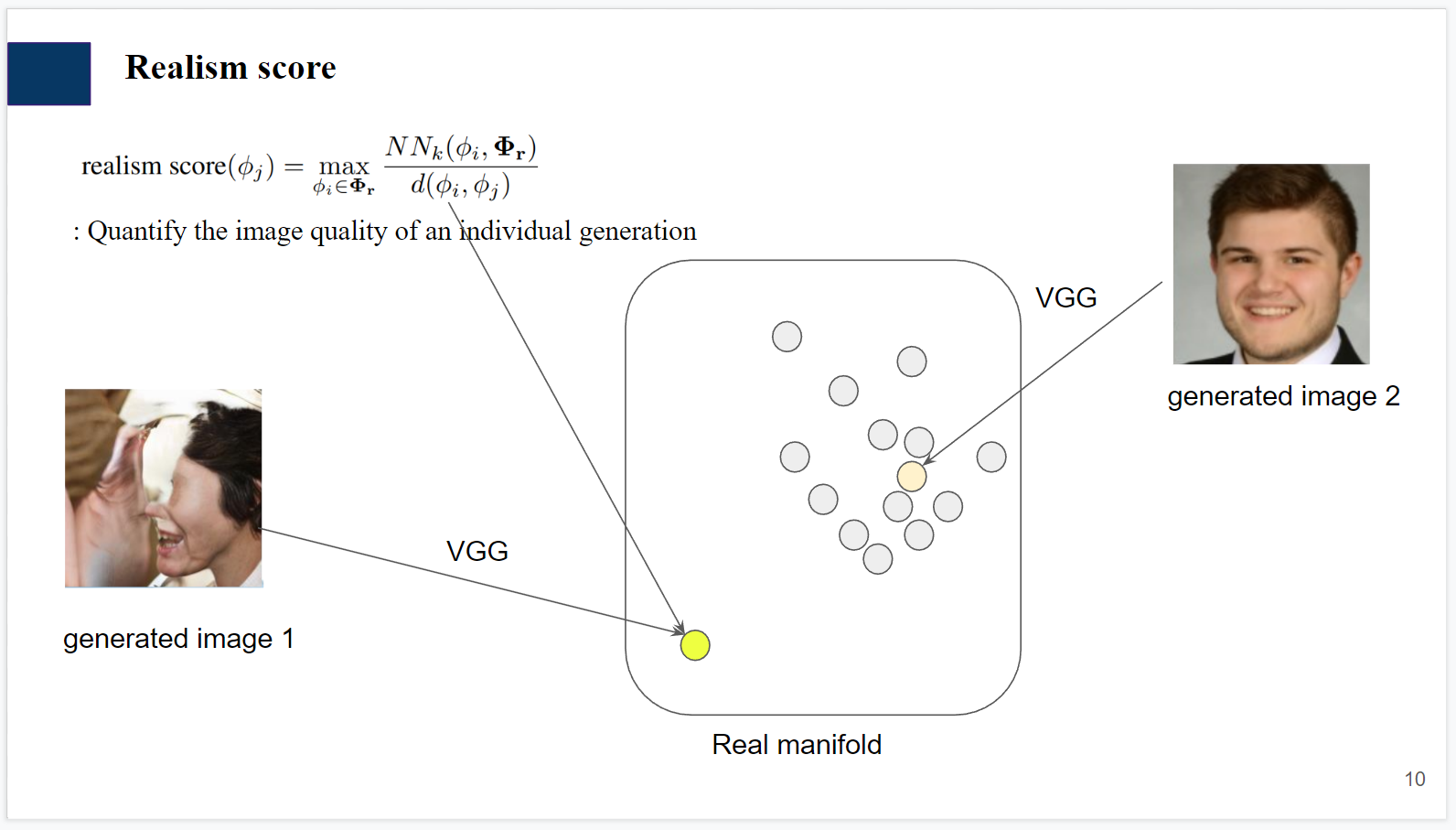
Generated1 을 임베딩하면 nearest real과의 distance↑, nearest neighbor의 radius↓ -> realism score 0.1

Generated2 을 임베딩하면 nearest real과의 distance↓, nearest neighbor의 radius soso -> realism score >>0.1

 

하지만 본 메트릭으론 이미지의 rare함을 측정하기엔 문제의 소지가 있음.

 

Countercase : 
The effect of the radius is depressed by the effect of the distance between the real and the fake sample.
If the radius of the k-NN sphere is small when the distance between fake sample and a real sample is also very small, 
Realism(=rarity) score would be large.

 

직관적으로 이해가 안된다면, 뒤로 넘어가도 무방하다.

 

 

Rarity score

---

Real의 typical한 샘플들은, 고만고만한 오밀조밀한 manifold 공간에 모여있다에서 직관을 얻어 rarity score를 얻었다고 한다.

 

rarity score 수식 설명

Individual generated sample이 만약 real의  hypersphere들에 속한다면,  속했던 hypersphere 의 최소 radius가 곧 rarity score가 됨.

 

g2는 r2, r3의 hypersphere 모두에 속하지만, r2의 sphere의 반지름이 더 작으므로 해당 반지름 값이 rarity score가 될 것.

(직관적으로 r2 샘플 주변에 파란 점(real)들이 많은 걸 보아, mean latent 부근이라 추측됨.)

 

 

 

a : g1이 오직 r1의 boundary에만 갇혀있는 경우. (rarity score 높음. r1은 radius가 큰 unique one 이기에.)

b: rarity score skw음

c: 어느 sphere에도 들어가지 못하는 g3은, 취급하지 않는다. real이라고 볼 수 없는 artifact 이미지는 애초에 rare함 고려를 해버리지 않음.

 

The choice of K

---

Spearman 상관계수 이용, 적당한 K를 정한 합당성에 대한 부분.

 

(논문의 설명이 이해하기 쉽지 않았음. 오픈 리뷰에서 왜 이 부분은 이야기가 안나왔는지 모르겠다.)

 

빨간 부분부터 보자면, K=1 , 1~10의 상관계수를 비교한 부분이다. 비슷한 범위의 K와는 correlation이 높고, sparse해질수록 차이가 난다고 함.

for example) (검은 점이 원 중앙에 있다고 생각하기.. 그림 잘 못 그렸음)

 

(fake들이 초록색 boundary안에서만 생성된다고 할 때), K=1, K=1의 correlation은 0이다.

K=1, K=2는 sphere 1의 두 번째 radius가 크므로 correlation이 이전 경우보다 떨어질것이다.

세 번째는 더 떨어질 것이다. 

but correlation은 k=1 , k=2 k=3 에서 어느 정도 높게 유지될 것이고, k=10 이렇게 커지면 correlation이 작아질 것이다.

 

 

두 번째 그림 .. 이해하는데 상당히 오래걸렸다.

The second plot in Figure 3 shows the average rank correlation between k = 1 and 1 ≤ k′ ≤ 10. Each color indicates the target generations in Mi. Please note that Mi ⊂ Mj for i ≤ j and the rank correlation changes dramatically for the cases in Mj \ Mi.

 

요약 : k>i (generated sample 생성되는 범위 지정해줌) 에 대해 consistent.

 

각 선들이 manifold1(k=1 boundary), maniford2(k=2 boundary) 에 generated sample 생성됨을 의미.

 

case들을 하나하나 살펴보면,

 

case1. (좌하단 네모박스 부근 집중) 

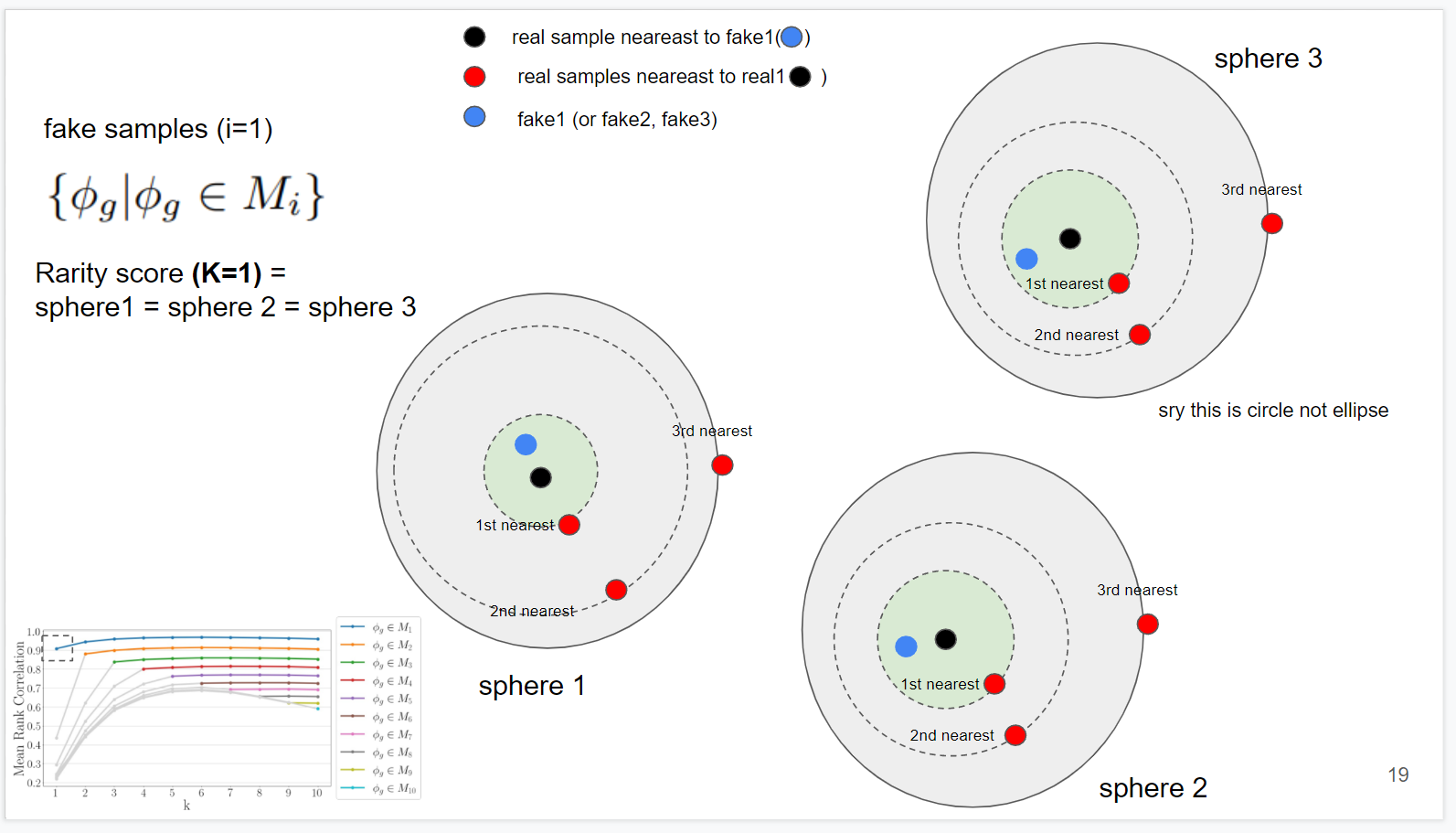
fake들은 M1, 즉 k=1(1st nearest) boundary 안에 생성됨.

k=1일 때 out of manifold 없음, 정확하게 radius 측정 가능.

따라서 k=1 과  k=1~10의 mean rank와  average rank correlation을 측정하면, 높은값 나올것. (네모박스 안의 점)

 

M1에 대해 k=2 과  k=1~10의 mean rank와  average rank correlation을 측정 역시 높을 값 나올것 (네모 박스 바로 오른쪽 점)

 

 

case2. (좌하단 네모박스 부근 집중) 

(k=1, M2 일 때)
M2는 K=1의 boundary 밖에 생성됨.

out of manifold가 두 sphere에 존재하고 rank를 정확하게 못만듦.

 

이 부정확한 rank와,  k=1~10의 mean rank와  average rank correlation을 측정하면, 엄청 낮은 값 나올 것

 

 

case 3.

(M2, k=2 일 때)

 

generated가 다시 k의 boundary(초록색) 에 속하므로 out of manifold 없고, rank 정확한 값 나올것.

 

따라서 k=2 과  k=1~10의 mean rank와  average rank correlation을 측정하면, 높은값 나올것. 

하지만 case 2가  k=1~10의 mean rank 값 구할때 트롤링 했기에 전체적인 correlation은 M1 보다 낮은 모습

 

이 case들의 반복이다.

i<k일 떄 correlation 이 consistent함. 에 집중하면 될듯함.

 

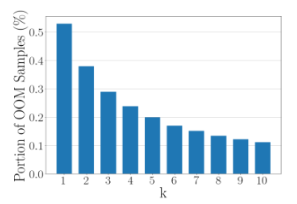
k=1,2로주면 OOM이 너무 많아진다. real의 manifold 구성하기엔 radius들이 너무 작아짐.

 

 

Experiment

---

 

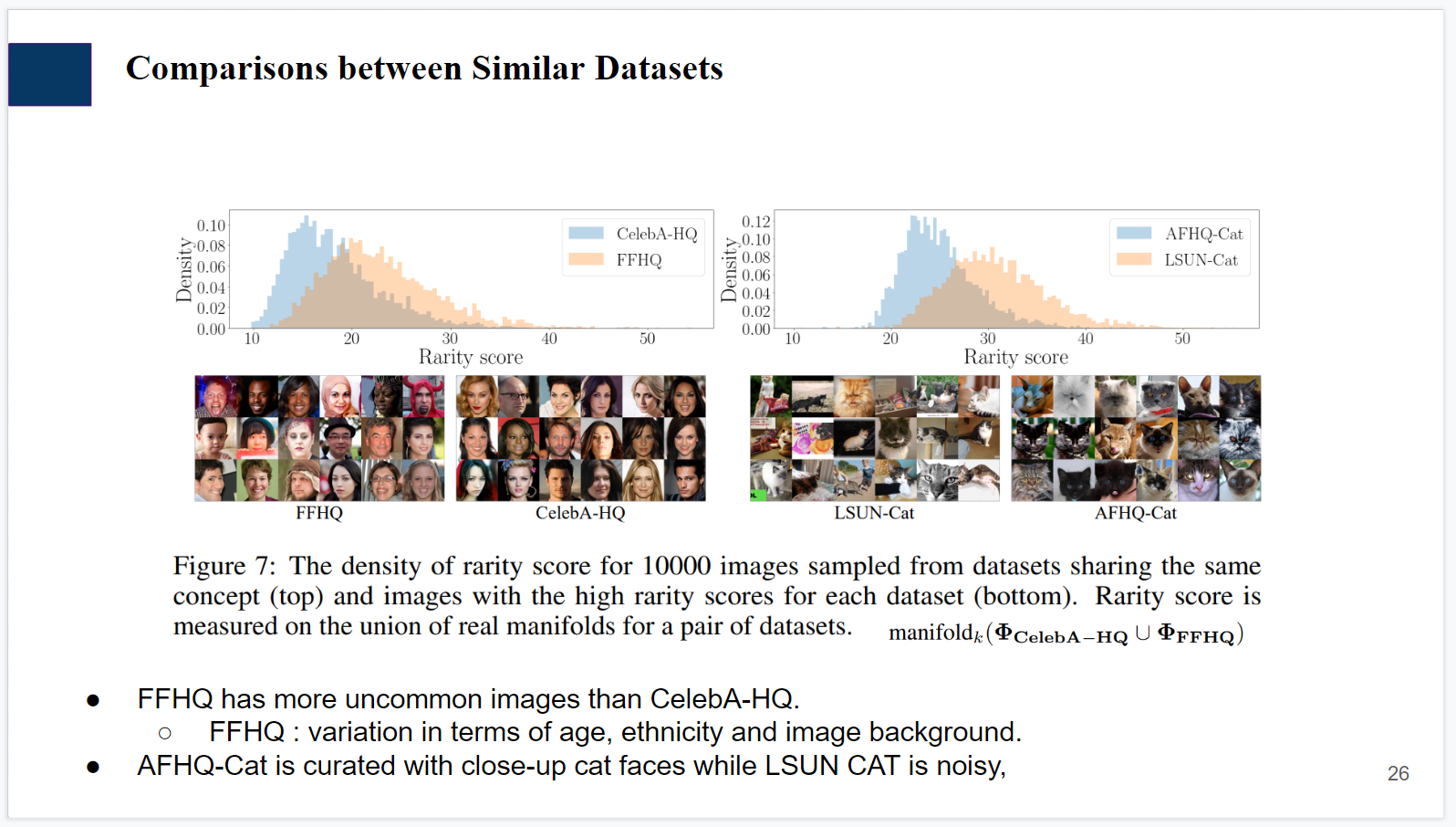
Conclusion

---

이 논문의 contribution

1. Can evaluate rarity of an individual image rather than a set of images.
2. Can be applied to compare between generative models or datasets in terms of the density of the rare samples.

 

내 생각

My opinion

• Real 수가 적으면 모든 face공간을 span하지 못해서 rarity score도 부정확할텐데, 최소 샘플 수에 대한 실험 X
• OOM 고려 x < 샘플 적으면 문제소지 생길듯? (real 해보이는 샘플도 제외할듯한 느낌)
• rarity score 23점 <- 얼마나 높은건지 감 잡기 어려움 like FID